| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- Client-Side Navigation
- Passed by Value
- CPU와 GPU의 차이점
- 식별자란
- 유령 의존성
- NextJs
- 프로젝트
- 광고지구
- Mac OS NVM
- JavaScript
- 원티트 프리온보딩인턴십 1주차
- 향해99
- jsEvent Loop
- lgcns camp
- Til
- react
- CloudFront 무효화
- NVM
- react portal
- git
- Node
- 원티드인턴십
- 알고리즘
- 원티드프리온보딩
- Redux
- next/link
- lg cns am inspire camp
- JS
- 회고록
- lg cns am inspire camp 2기
- Today
- Total
SUIN
시간복잡도와 공간복잡도 / 점근 표기법 / 빅오 표기법 / P-NP 본문
알고리즘이란 문제를 해결하기 위한 방법이라고 할 수 있다
하나의 문제를 풀 때 여러 가지의 코드를 사용해서 풀게 되는데 알고리즘의 계산복잡도는 시간복잡도와 공간복잡도 두 가지의 척도로 표현될 수 있다.
좋은 알고리즘은 실행 시간도 짧고, 저장 공간도 적게 쓰는 알고리즘이지만 두 복잡도는 서로 반비례하기 때문에 두 가지를 모두 만족할 수 없다
시간복잡도와 공간복잡도 사이에서 최적의 알고리즘을 선택해야 하는데 최근 하드웨어가 발전함에 따라 대용량 시스템이 보편화되면서 연산속도가 빨라지고 가격도 많이 낮아지며 공간복잡도보다는 시간복잡도를 조금 더 중요시하는 경향이 있다.
"시간복잡도를 고려하여 개발하게 된다면 같은 기능이라도 더 빨리 수행하는 코드를 작성할 수 있으며 서비스품질에도 영향을 줄 수 있다"
그럼 시간복잡도와 공간복잡도에 대해서 알아보자
시간복잡도 : 문제를 해결하는 데 걸리는 시간과 입력의 함수관계 (알고리즘을 푸는 시간 )
공간복잡도 : 문제를 해결하는 데 실행하여 종료할 때까지 필요한 기억장치(메모리)의 크기
시간복잡도
- 문제를 해결하는데 걸리는 시간과 입력의 함수관계 (알고리즘을 푸는 시간)
시간 복잡도는 보통의 경우 점근 표기법으로 사용되는데 주로 사용되는 점근 표기법은 아래와 같이 3가지가 있다.


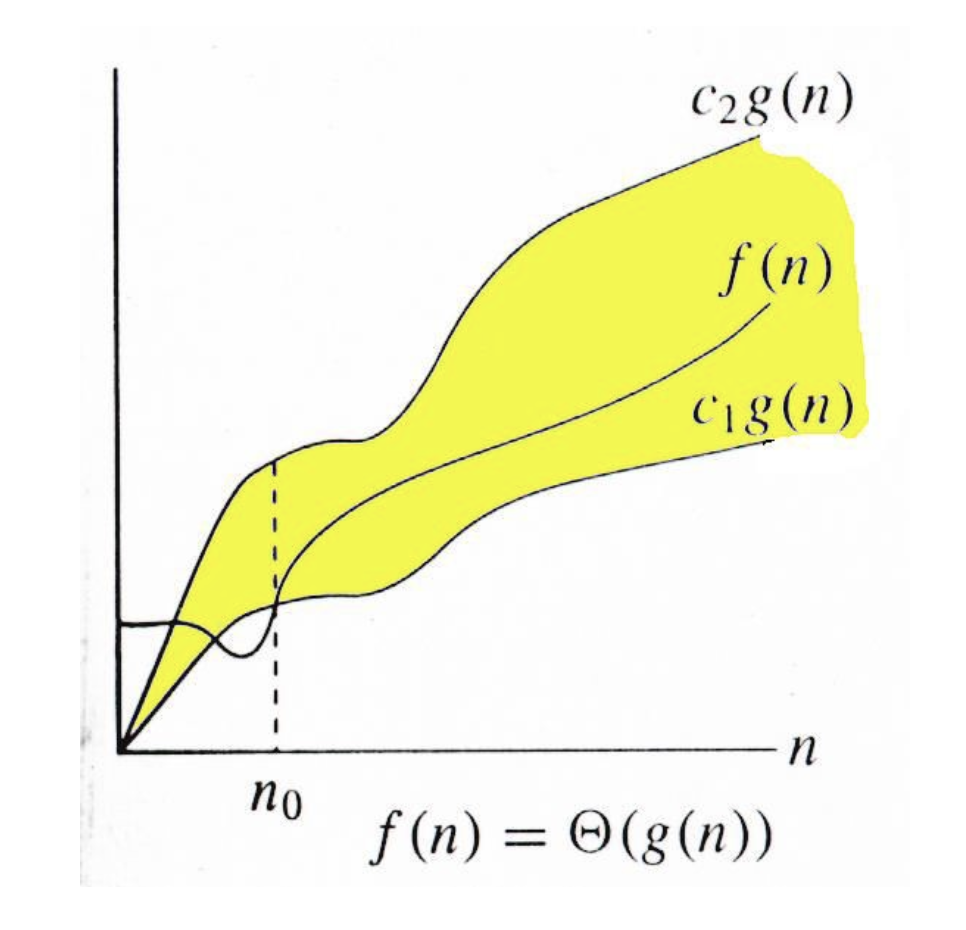
- Big-O표기법 / O(N) : 빅오 표기법은 알고리즘 최악의 실행시간을 표기
- Ω 표기법 / Ω(N) : 오메가 표기법은 알고리즘 최상의 실행시간을 표기
- Θ 표기법 / Θ(N) : 세타 표기법은 알고리즘 평균 실행시간을 표기
3가지의 방법 중 빅오 표기법이 많이 사용되는 점근 표기법이다 그 이유는 무엇일까?
Omege : 어떤 알고리즘이어도 만족할만한 결과를 주기 때문에 정확한 비교를 할 수 없다
Theta : 평균적인 상황을 잘 가정할 수 없다 (어떤 게 평균적인 상황이라고 정의할 수 없기 때문)
이러한 상황으로 우리는 최악의 경우를 염두하여 Big-O 표기법으로 알고리즘을 계산하게 된다.
빅오 표기법(Big-O)은 시간 복잡도를 나타내는 표기법 중 하나로 'O(입력)'으로 표기한다. 빅오 표기법의 성능 순서는 다음과 같이 나타낼 수 있다.
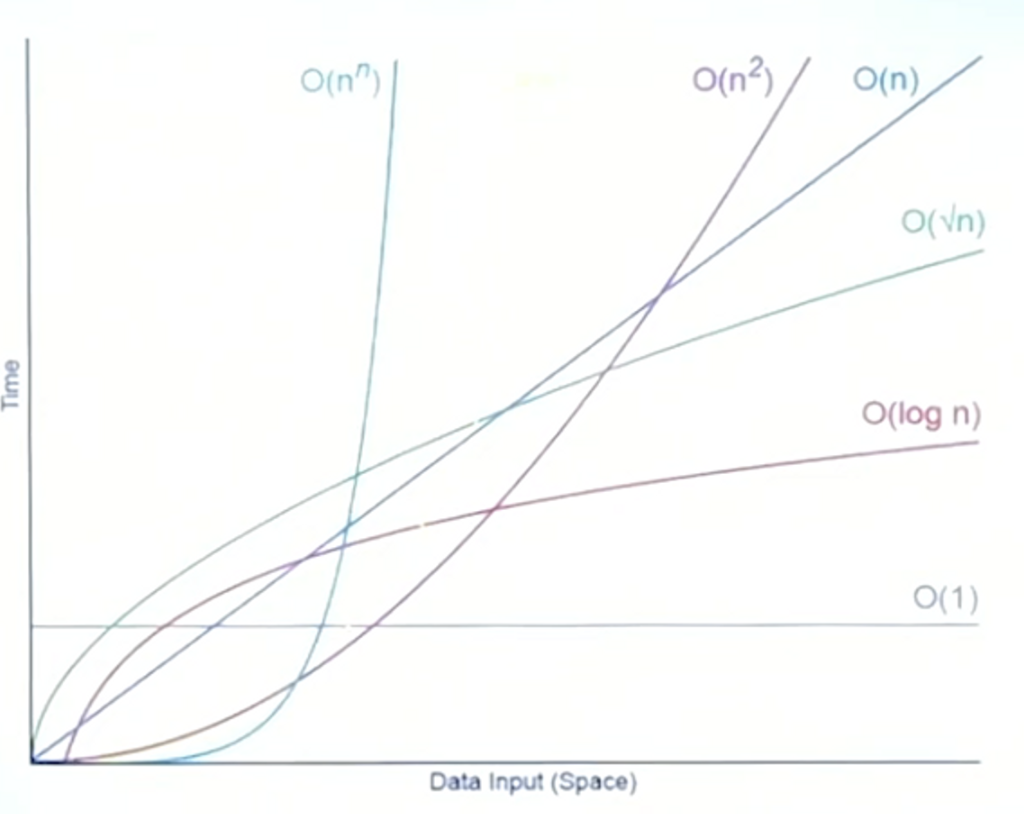

가장 왼쪽 O(1)으로 갈수록 실행 횟수가 적은 것 / 시간 복잡도가 낮은 것이라 말할 수 있고, 가장 오른쪽 O(n!)으로 갈수록 실행 횟수가 많은 것 / 시간 복잡도가 높은 것이라고 말할 수 있다.
시간복잡도 계산하기
시간복잡도를 계산하는 데 있어서 가장 중요한 것은 핵심이 되는 연산을 찾는 것!이다
빅오 표기법은 상수에 신경 쓰지 않으며 함수의 디테일보다는 러프하게 어떻게 이 함수가 동작한느지가 중요하다.
예 )
n² + 2n → O(n²)
2 n² + 3n → O(n²)
-> n² + 2n의 핵심이 되는 연산은 n²이며 2n의 경우 n²에 의해 무시될 수 있다.
O(1) 상수 시간
: 알고리즘이 입력에 관계없이 연산이 수행된다. 즉 입력 데이터의 크기에 상관없이 일정한 시간이 걸린다.
function BigO(n){
console.log("Hello Big-O");
}
O(n) 선형 시간
: 알고리즘이 입력한 개수인 n만큼 수행된다. 즉 입력 데이터가 증가할수록 처리시간도 증가한다.
function BigO(n){
for(let i=0; i<n; i++){
console.log(i);
}
}만약 2개의 출력이 존재할 경우 O(2n) 이 아닌 O(n)이다
function BigO(n){
for(let i=0; i<n; i++){
console.log(i);
console.log(i);
}
}
O(n^2) 2차 시간
: 알고리즘이 입력한 개수의 n^2만큼 수행된다. 즉 입력 데이터가 증가할수록 처리시간이 제곱 배로 증가한다.
function BigO(n){
for(let i=0; i<n; i++){
console.log(i);
for(let j=0; j<n; j++){
console.log(j);
}
}
}
현실적 알고리즘, 비현실적 알고리즘

위의 그래프에서도 보이듯 빅오 표기법에서 O(n²)처럼 지수형태로 올라가는 알고리즘을 우리는 풀 수 없는 알고리즘(비현실적 알고리즘)이라 한다.
현실적과 비현실적
현실적 알고리즘(Polynomial complexity) = P
- 상식 선에서 풀 수 있는 문제
비현실적 알고리즘(Nondeterministic Polynomial complexity)= NP
- 복잡도가 factorial이나 지수 형태로 올라가는 알고리즘
- 해밀턴 경로 문제 (모든 경우가 한 번만 지나는 경우)

수학계의 최종 보스인 밀레니엄 문제 중 하나로, P 집합과 NP 집합이 같은지 다른지를 증명해야 하는 문제다. P 집합은 이미 NP의 부분집합이므로, 모든 NP 문제가 P 문제라는 것을 밝히면 P 집합과 NP 집합은 같은 것이 된다.
예 ) NP문제 (소인수 분해)
1번 . 3*7 =21
→ 굉장히 빨리 구할 수 있다
2번. 21 =?
→ 21만 주어졌을 때 어떤 소수의 곱인지 오랜 시간이 걸린다.(21이 아닌 더 큰 숫자의 경우 더 오랜 시간이 걸릴 것이다.)
그럼 우리는 왜 비현실적 복잡도를 알아야 하는가?
바로 전 세계에 비밀보안에 사용되는 공개키와 비밀키가 소인수 분해의 어려움(비현실적 시간 복잡도)을 이용한 예이기 때문이다


p*q = n(공개키)
n을 공개한다고 해도 p*q가 무궁무진하기 때문에 비밀키를 알 수 없다.
만약 P=NP 같다고 증명이 된다면? 보안이 되는 모든 공개키 비밀키 암호들이 의미가 없어질 것 이다
공간 복잡도
문제를 해결하는데 실행하여 종료할 때까지 필요한 기억장치(메모리)의 크기
공간 복잡도 계산하기
S(P) = c+Sp(n)
- c: 고정공간(코드의 저장공간, 단순변수, 고정크기의 구조변수, 상수)
- Sp(n) : 가변공간(동적으로 필요한 공간)
O(1)
: i라는 변수에 0을 할당한 것 외에, 공간을 차지하는 것이 없다
const spaceComplexity = (array) => {
for (let i = 0; i < array.length; i++) {
console.log(array[i]);
}
};O(n)
: 반복문이 n만큼 도는 동안 공간이 하나씩 추가된다.
const spaceComplexity3 = (n) => {
let array = [];
for (let i = 0; i < n; i++) {
array[i] = i;
}
return array;
};
참고
https://namu.wiki/w/P-NP%20%EB%AC%B8%EC%A0%9C
https://velog.io/@hahan/Algorithm-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84-%EB%B9%85%EC%98%A4-%ED%91%9C%EA%B8%B0%EB%B2%95
https://velog.io/@igun0423/Javascript-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B3%B5%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84
https://www.youtube.com/watch?v=LBR9K8NPtvQ
https://www.youtube.com/watch?v=IEH3YA2Nn4Q
